Sabe quando você não acompanha com frequência uma modalidade, e, na hora de assistir às Olimpíadas na TV, começa a fazer um turbilhão de perguntas? O g1 está aqui para resolver um dos mistérios que assombram a cabeça dos espectadores amadores de atletismo.
?♂️➡️?♀️➡️Por que os corredores não dão a largada a partir do mesmo ponto nas provas ? O que justifica que alguns comecem mais à frente, se a linha de chegada é a mesma para todos?
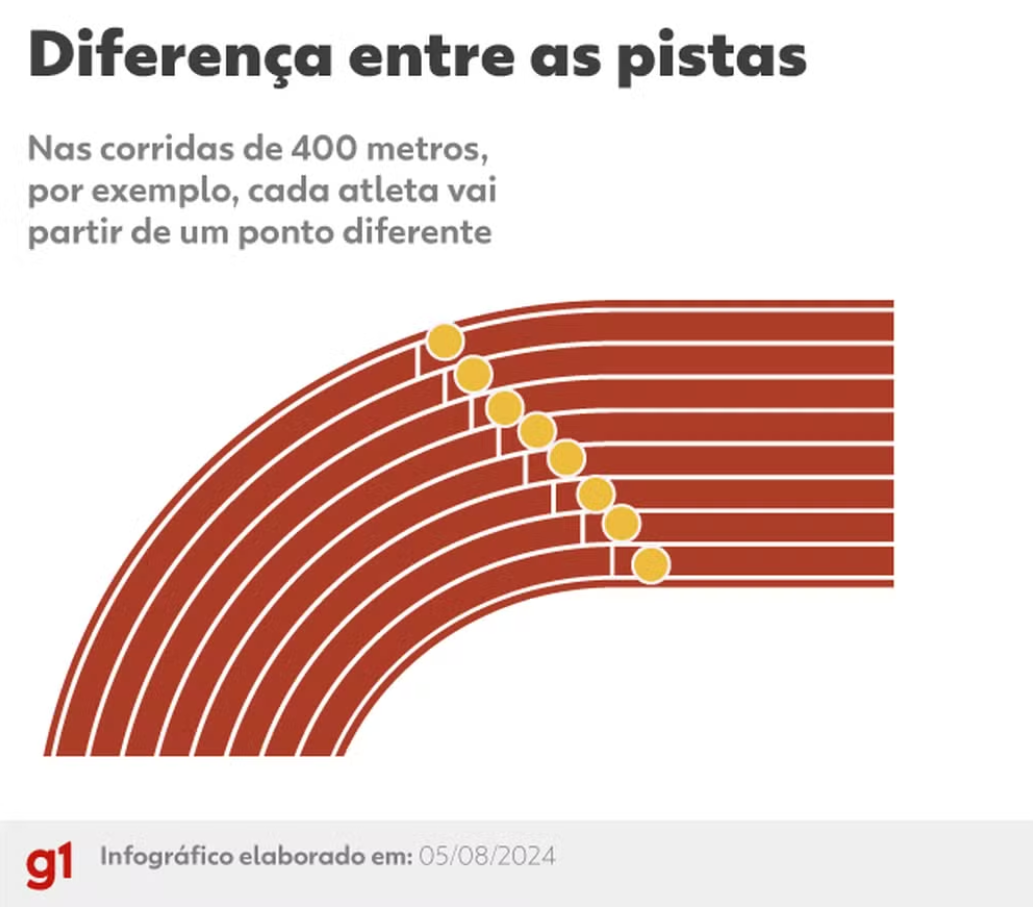
A resposta está na matemática. Vamos pensar nas provas de velocidade: tanto na de 200 metros quanto na de 400 metros, é preciso “escalonar” os atletas em posições diferentes no começo (veja imagem abaixo).
?Por quê? É que as pistas formam uma elipse (ou seja, não são retas, e sim “ovais”). E o fato de haver uma curva nas extremidades faz com que o comprimento de cada raia seja diferente.
Pense na número 1, que é a mais central, “de dentro”: quem correr nela percorrerá a distância exata proposta pela prova.
Já o corredor na raia 8, que fica mais “para fora”, encarará um percurso mais longo, porque o raio da circunferência que forma as curvas da pista é maior (explicaremos com detalhes mais adiante).
Compare o tamanho do arco 1 com o do 8:
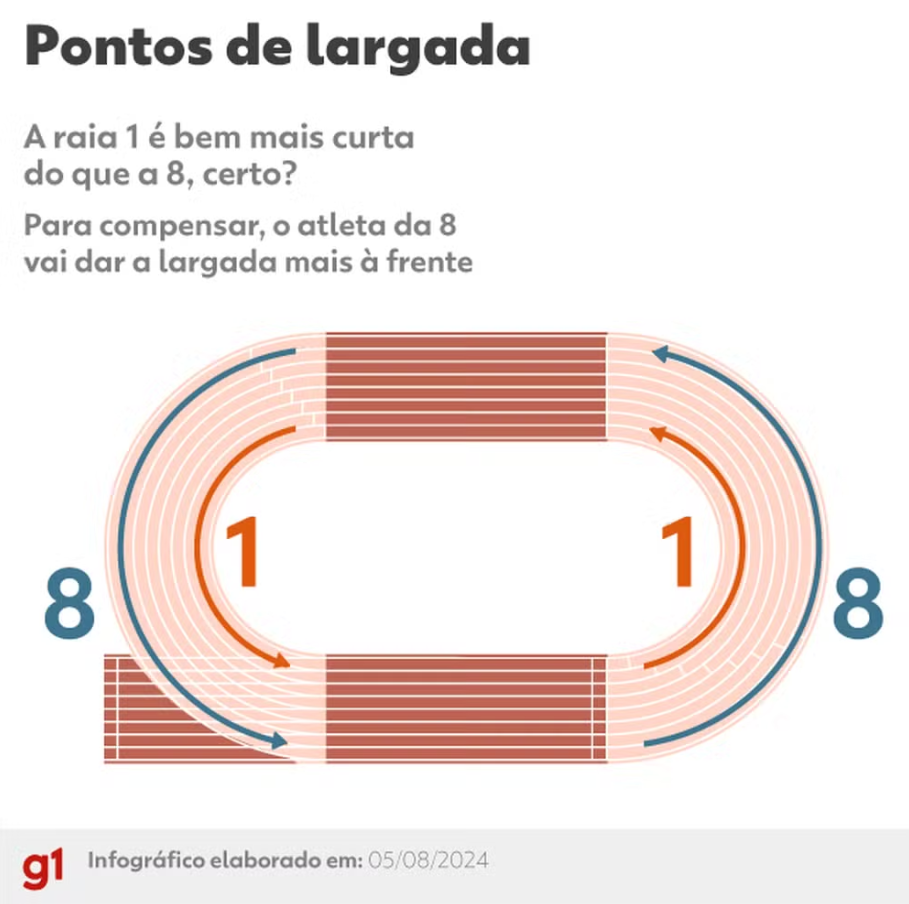
✅A forma de compensar essa diferença é justamente permitindo que os atletas das raias mais externas larguem à frente.
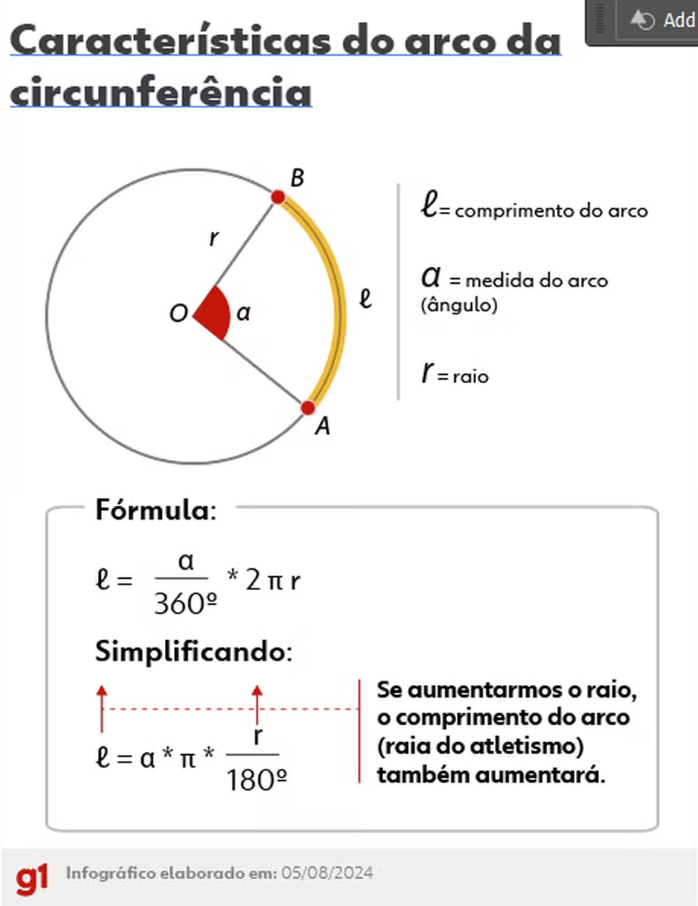
Fórmulas de matemática (dica para o Enem!)
O professor de matemática Thiago de Araújo, do Curso Anglo, explica que o conceito-chave para entender por que cada raia tem um tamanho é o comprimento do arco.
Visualmente, você deve ter percebido que os percursos ficariam realmente muito diferentes em cada raia. Mas vamos ver a justificativa numérica:
1- A fórmula para calcular o comprimento total de uma circunferência é C = 2 . π . raio.
2- Pense que o arco (representado por ℓ, é aquela curvinha no canto da pista) é um pedacinho de uma circunferência de 360º. Para calcular o comprimento dele, é preciso, primeiramente, observar o ângulo formado no centro (α).
Vamos saber, então, qual a fração que o ângulo representa do total (α/360º) e multiplicar pelo comprimento da circunferência (2 π r).
Ou seja: ℓ = α/360º * 2 π r
Simplificando, chegamos a ℓ = α * π * r / 180º.
Portanto: quanto maior o raio, maior será o arco.
3- Nas raias mais externas, o raio da circunferência é maior. Logo, o comprimento do arco também é maior.
Por isso que os atletas vão partir de pontos diferentes: para que essas diferenças sejam compensadas, e todos corram a mesma distância.
Questão do Enem: você seria medalhista?
Na edição de 2011, a prova de matemática do Exame Nacional do Ensino Médio (Enem) abordou exatamente a questão das diferentes raias do atletismo. E aí, você acertaria? Veja a resolução mais abaixo.
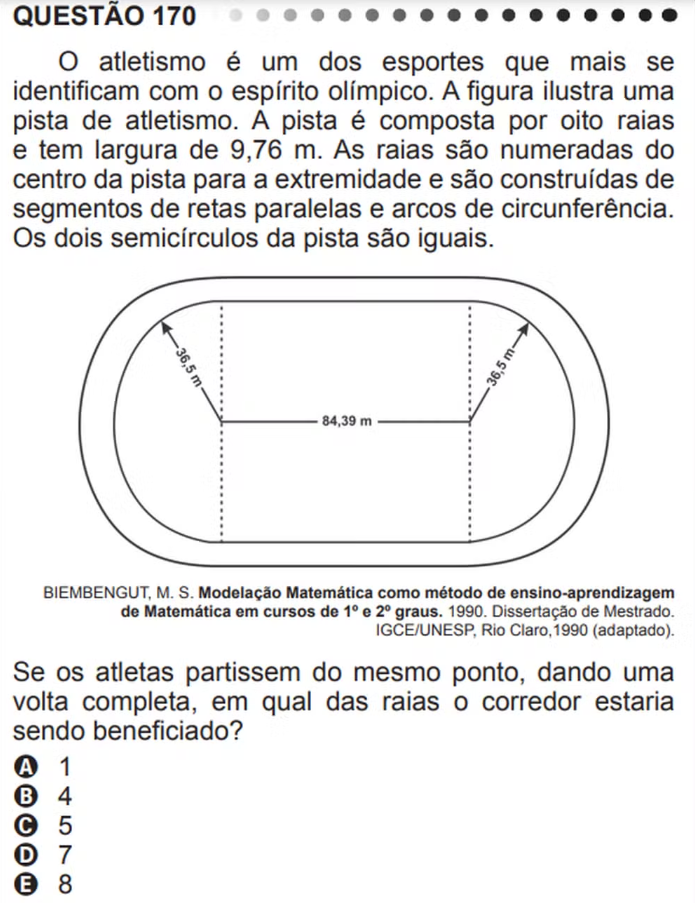
Como mostramos mais acima, quanto menor o raio, menor o comprimento do arco (e do percurso). Portanto, o corredor da raia número 1, que estaria no percurso mais central e curto, seria beneficiado.
Resposta: A










